Pentominoes
Pentominoes are like dominoes, except five squares are used to make each piece. There are twelve different shapes that can be made from five squares.
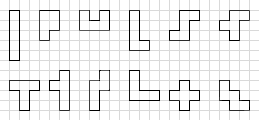
They are sometimes given simple letter names:
I P U L Z R
T Y N V X W
A set of these twelve shapes covers 12 times 5 or 60 squares in all. A puzzle is to fit a set of the twelve shapes into 6 by 10, 5 by 12, 4 by 15, or 3 by 20 frames. Any shape frame that has an area of 60 squares will also do. Such puzzles are actually commercially available.
It is difficult for me to solve this puzzle. It makes an ideal problem for a computer. I first wrote a program to find a solution to this puzzle in 1975. It turns out that there are typically many, many different solutions to these puzzles.
To cover large areas, you need to use many sets of the twelve shapes. The easiest way is to fit them into the frames mentioned above, then arrange these rectangular frames to fill the area desired. However if you do this, you immediately see the outlines of the frames. I wanted a pattern that would not easily reveal boring rectangles when I looked at it. I wanted to use an equal number of each shape. I wanted each shape evenly spread out.
The answer ? Recursion. Fit the twelve pieces into twelve frames each shaped like one of the pieces themselves. I describe the details of this technique in the Project: Fornax article.
I have done three needlepoint pieces using this technique, and think this approach can be used best on large projects. I hope one day to hook a large rug based on an intricate pattern of pentominoes.