Project: Fornax
Fornax is an attempt to make a visually interesting design entirely out of pentomino puzzle pieces. These are described on the Pentomino puzzles page.
The first step is to design the layout of all of the pieces. The second step is to color them in.
Step1 - layout of pieces
The secret, as you can read in my "Needlepoint Now" article, is to use recursion. That is: to fit smaller pentomino pieces into frames shaped like pentomino pieces. How small should the smaller pieces be? The ratios three to one and four to one work well. If the ratio is four to one, then 16 of the smaller pieces are needed to fit onto each of the larger frames. If the ratio is three to one, then only 9 are needed. The area math works out, but can you actually find an arrangement of pieces to fit into each of the larger pentomino frames?
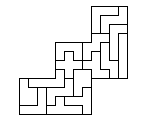
The answer is yes, in all cases you can (although some frame shapes
and sizes are more easily filled than others). Here is an example of
16 smaller pentominoes fit into a larger "W" pentomino frame.
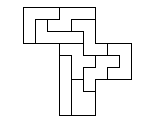
Here is an example of 9 smaller pentominoes fit into a larger "R"
pentomino frame.
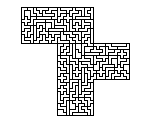
The idea of recursion comes into play when you take each of the
smaller pieces and fit even smaller pieces into them. Here is the
previous "R" exploded into a second level of pieces.
Now the design question is: What size and shape frame do you start with, and how far do you go fitting smaller and smaller pieces into it?
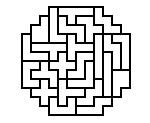 I wanted a symmetrical shape, and I wanted to use all of the
pentominoes at the top level. Each pentomino is 5 squares, and there
are 12 of them, so any frame must have an area that is a multiple of
60 squares. If you use two sets of pentominoes, then you need an area
of 120 squares. One way to do this is a square 12 x 12, with 24
knocked out (6 on each corner) like this.
I wanted a symmetrical shape, and I wanted to use all of the
pentominoes at the top level. Each pentomino is 5 squares, and there
are 12 of them, so any frame must have an area that is a multiple of
60 squares. If you use two sets of pentominoes, then you need an area
of 120 squares. One way to do this is a square 12 x 12, with 24
knocked out (6 on each corner) like this.
This frame has the added benefit that you can put four "W" pentomino pieces in the corners. Now you have a 12 x 12 square with one square knocked out of each corner. If you are thinking of recursion, you see that you can use a 1/12 scale version of this figure in each of the corners. Happily, 1/12 is 1/3 x 1/4, so we know we can fit small pentomino shapes into these corners.
We now have a frame with 28 large pentominoes fit in. We can potentially have pentominoes at a scale of 1:1, 1:3, 1:4, or 1:12. If we make the smallest pentomino 20 stitches, (each square is two stitches on a side) then the overall length of a side is 12 (big squares) x 4 (first level small scale pieces) x 3 (second level small scale pieces of 1/12) x 2 (stitches per square side) or 288 stitches. Using 14 guage canvas, this works out to 20 1/2 inches. A manageable size.
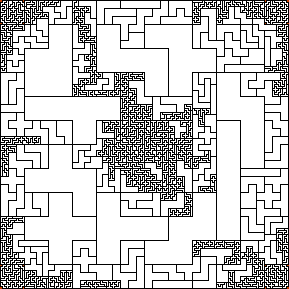
The Fornax design mapped out
Step2 - color them in
Instead of dissolving all of the large pieces into smaller pieces to make a large intricate puzzle (like I did on my first pentomino piece), I wanted a visually appealing design.
 This is where the math
stops, and inspiration needs to take over. The idea for this piece
popped into my head while barreling down the runway in a jet, taking
off on a vacation to New York City.
This is where the math
stops, and inspiration needs to take over. The idea for this piece
popped into my head while barreling down the runway in a jet, taking
off on a vacation to New York City.
Some pieces are left un-touched as large blocks. Others are dissolved as 1/3, some at 1/4, and some of those are further dissolved to 1/12 size. The color scheme complements the arrangement of sizes. This design suggests something very specific to me. But that would be telling. Each viewer can see what they want.
Here is the completed piece. A larger image is
here.
I describe what pentominos are in this article.

